Random Forests

Decision Trees

Pros

  • Interpretable
  • Simple
  • Classification or Regression

Cons

  • Poor accuracy
  • High variance

Bias vs Variance

Bias-Variance Trade-off

$Error = Variance + Bias^2 + noise$

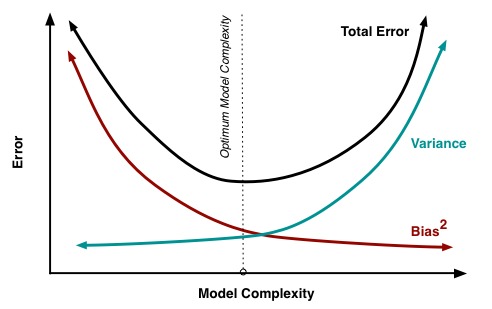
Reduce bias: Build more complex models

Reduce variance: Use a lot of data or simple model

How to reduce the error caused by noise?

Fisher Rolling in his Grave

Bagging

Averaging a set of observations reduces variance.

But we only have one training set ... or do we?

Bootstrap

Simulate new datasets:

Take samples (with replacement) from original training set

Repeat $n$ times

Bootstrap visualization

Sample has $n$ elements.

Probability of getting picked: $\frac{1}{n}$

Probability of not getting picked: $1-\frac{1}{n}$

If you sample $n$ elements with replacement, the probability for each element of not getting picked in the sample is: $(1-\frac{1}{n})^n$

As ${n\to\infty}$, this probability approaches $\frac{1}{e}\approx.368$

Thus, $0.632$ of the data points in your original sample show up in the Bootstrap sample (the other $0.368$ won't be present in it)

Bagging

Train a tree on each bootstrap sample, and average their predictions (Bootstrap Aggregating)

Random Forests

Like bagging, but removes correlation among trees.

At each split, considers only a subset of predictors.

Notes:
Random forests typically consider $\sqrt{\textrm{number of features}}$ or $1/3$ at each split (if 10 features, then it considers ~3 features), and picks the best one.

Slide credit G. Calmattes

Random Forests

Slide credit G. Calmattes

A Step away from Interpretation

  • How do you model a vote from many trees?
  • Improved prediction, reduced interpretation
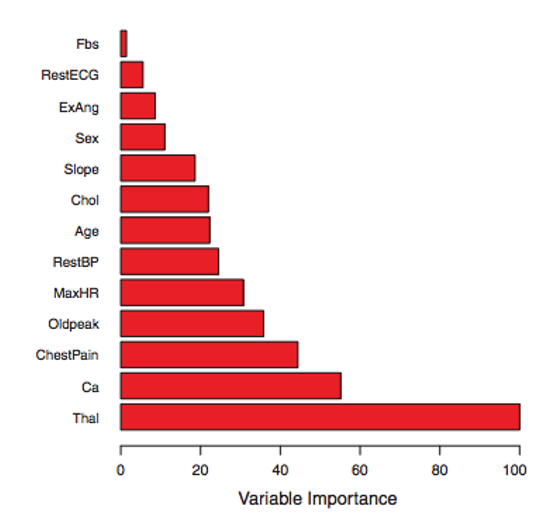
  • Feature importance
    • Mean decrease in Gini index relative to the max
    • Show’s influence not directionality
    • Bucketing importance on highly dimensional data

Hyperparameter Selection

What is a hyperparameter?

Which dataset should we use to select hyperparameters? Train? Test?

Validation Dataset

Split the dataset into three!

  • Train on the training set
  • Select hyperparameters based on performance of the validation set
  • Test on test set

What if you don't have enough data to split in 3 separate sets?

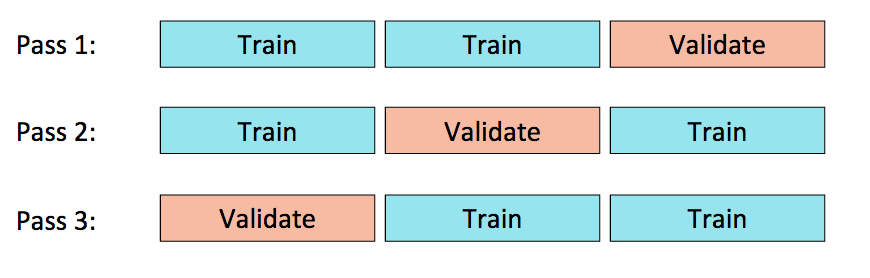
K-Fold Cross Validation

Grid Search

Try various hyperparameter settings to find the optimal combination

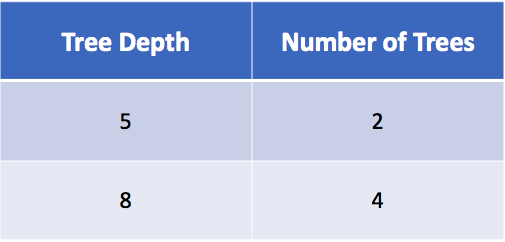
How many models will this build (k = 3)?

Random Forest Lab

Problems with Grid Search

Exhaustive enumeration is expensive

You have to determine the exact search space

Past information on good hyperparameters isn’t used

So what if...

  • You have a training budget
  • You have a lot of hyperparameters to tune
  • Want to pick your hyperparameters based on past results

Hyperopt

Optimization over awkward search spaces

Serial and parallel

Spark integration

3 algorithms

  • Random Search
  • Tree of Parzen Estimators (TPE)
  • Adaptive TPE

Paper

Random Search

Paper

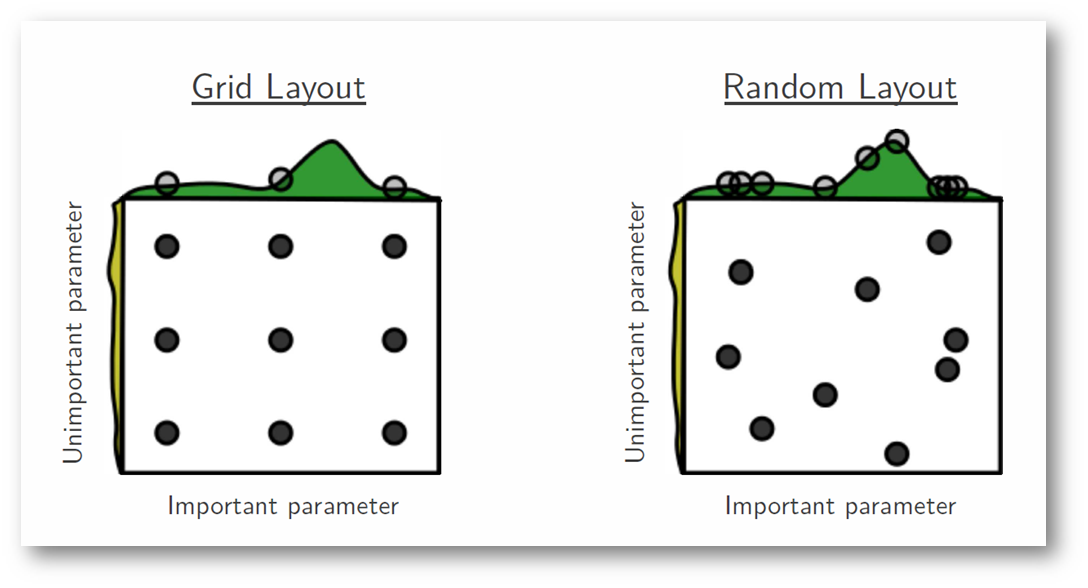
Generally outperforms exhaustive search

Can struggle with on some datasets (e.g. convex spaces)

Tree of Parzen Estimators

Meta-learner, Baysian process

Non-parametric densities

Returns candidate hyperparameters based on best Expected Improvement (EI)

Provide a range and distribution for continuous and discrete values

Adaptive TPE better tunes the search space (e.g. freezes hyperparameters, tunes # random trials before TPE)

Other Ensemble Models

Gradient Boosted Decision Trees

Sequential method

Fit trees to residuals (on first iteration, residuals are the true predictions)

Idea: build tree more slowly

These trees are NOT independent of each other

GBDT

Y Prediction Residual
$40$ $35$ $5$
$60$ $67$ $-7$
$30$ $28$ $2$
$33$ $32$ $1$
$25$ $27$ $-2$
Y Prediction Residual
$5$ $3$ $2$
$-7$ $-4$ $-3$
$2$ $3$ $-1$
$1$ $0$ $1$
$-2$ $-2$ $0$

Y Prediction
$40$ $38$
$60$ $63$
$30$ $31$
$33$ $32$
$25$ $25$

Boosting vs Random Forest

Boosting starts with high bias, low variance and works right

RF starts with high variance and reduces it by averaging many trees

Kaggle

Data Science and Machine Learning Competition site

XGBoost one of most winning solutions

https://www.kaggle.com/

What is XGBoost?

Boosted trees with…

  • Weighted quantile sketch for approximative learning
  • Smart cache access and data compression
  • A sparsity-aware algorithm for sparse data
  • Sharding

10x speed increase

Scale in the billions

Parallelized and distributed

Resources